宇宙は、無限か有限か？夜空はなぜ暗いのか解明の一歩はニュートンの「りんご」にあった？

ryomiyagi

2019/12/16

私たちのまわりには空間が四方八方に広がっています。少なくとも、見た目にはどこまでも果てしなく続いているように思われます。果たしてこの空間は無限に続いているのでしょうか、それとも、十分に大きいだけで実際には有限に途切れているのでしょうか。現代科学が解明できない宇宙という謎めいた存在には、一体どれほどの可能性が秘められているのか？　最新の宇宙論から、私たちがいるのはどこなのか、根源的な問いに迫ります。

※本稿は、松原隆彦『宇宙は無限か有限か』（光文社新書）の一部を再編集したものです。

■ニュートンが考えた「無限宇宙」

地球が1年で太陽のまわりを1周するならば、視点が1年ごとに変化するため視差が生じ、恒星までの距離によって、その位置が1年周期で動いて見えるという、地動説を確立させ太陽以外の恒星までの距離を測る基準になった「年周視差」が、1838年に初めて測定された。

それよりもずっと前のことだが、ニュートンは自分の発見した万有引力の法則に基づいて、星が無限の空間にばらまかれているべきだと考えた。

万有引力の法則によれば、星々はお互いに引き合う。このことから、星が自然にどこか一ヶ所に集まってしまうのではないか、という疑問がすぐに浮かんでくる。

もしも星のばらまかれている範囲が限られていたら、確かにそうなるだろう。力学の法則によれば、星々は平均的に重心と呼ばれる場所へ向かって力を受ける。

重心とは、重さに関する中心のことである。最初にすべての星々を静止した状態にしておいても、この力を受けることで、すべての星が重心に向かって動き出すだろう。

だが、当時は星々が動いているという証拠もなく、また宇宙は永遠不変のものであるというのが常識であった。星が動かずに止まっているなら、重心があってはならないことになる。

星のばらまかれている範囲が有限であれば、重心がどこかに必ず存在する。一方、もし無限に宇宙が広ければ、空間のどの場所も平等になってしまうので、重心を定めようがなくなる。

こうして、星々が無限の宇宙空間に静止しているだろうと考えたのである。

■星が無限に広がっている理由は、「神の摂理」だから？

だが、このような無限に広がった星の配置は不安定だ。星々が無限に広がっているとき、ある一つの星はどちらの方向へも無限の力で引っ張られる。

星が止まっていられるのは、反対方向から引っ張られる力がすべて打ち消し合うためだが、この場合には無限の力と無限の力が打ち消し合う必要がある。

だが、どこかでその均衡が破れ、ちょっとでもその打ち消し合いが崩れると、星に力が働いて動き出す。そして、どこかで星が動き出すと、その星の動いた方向に星の数が増えていく。星の数が増えた場所では重力が強くなり、ますます他の星が集まってくる。こうして一気に星のある場所とない場所の違いが際立ってしまうことになる。

つまり、ニュートンの考えたような無限に広がった宇宙は可能だが、極めて微妙なバランスの上にしか成り立たないものなのだ。ニュートン自身もこのことに気づいていたが、その理由を合理的に説明することはできなかった。そして、最終的にこの宇宙が微妙なバランスを保っているのは、神の摂理なのだと述べるにとどまっている。

■夜空はなぜ暗いか

このようにして、無限に広がった宇宙の可能性が考えられるようになった。

だが、もし星々が無限の空間に均等にばらまかれているとすると、ひとつの矛盾のようなものが生じる。それは、そのように無限に続く空間を見ると、どの方向へ目を向けたとしても視線の先には必ず星が見えて、夜空全体が明るく輝くだろうということだ。

だが、実際の夜空は暗い。無限に続く宇宙では夜空全体が星の光で輝いているはずということは、次のようにしてわかる。

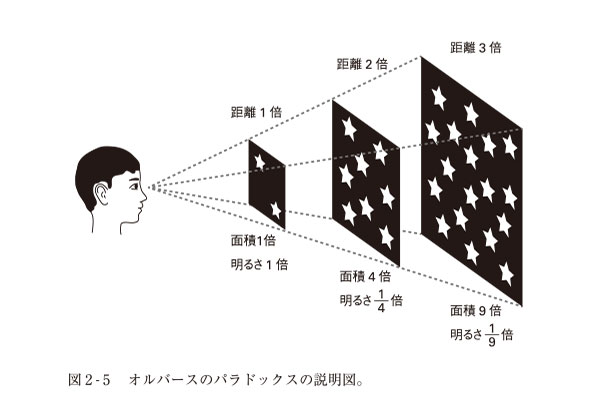
遠方になるほど、ひとつの星から出る光は暗く見えるが、遠方には星がたくさんある。ひとつの星から出る光の強さは距離の2乗に反比例して弱くなっていく。

一方、奥行き方向に決まった厚みを持つ体積を考えると、その中に入っている星の数は、視線に垂直な面の面積に比例するので、距離の2乗に比例して増えていく。星の光が弱くなる効果と、星の数が増える効果は打ち消し合う。

このため、近くにある星々からやってくる光のエネルギーも、遠くの星々からやってくる光のエネルギーも、空の決まった領域を見たときにそう変わらないことになるのだ。

ここで、もし星の光を無限の彼方まで見通せるならば、夜空の明るさは無限に明るくなる。

実際には手前にある星が後ろにある星を隠すので、無限の彼方までは見通せず、夜空の明るさは有限になるはずだ。結局、視線の先が必ずどこかにある星の表面にぶち当たるため、夜空全体が星の表面と同じ明るさで輝くはずなのである。

この問題は、天文学者ハインリヒ・オルバースによって1823年に述べられているため、「オルバースのパラドックス」と呼ばれている。だが、オルバースはこの問題に最初に気づいた人ではない。それは以前から知られている問題だった。

■「オルバースのパラドックス」の発見者は、オルバースではない？

コペルニクスの地動説をもとにして、星が無限に続く空間にばらまかれていると主張したディッグスは、すでにこの問題を考察している。

ただ、ディッグスは単に星が遠くにあって十分に暗いので夜空が明るく輝くことはないのだと誤って考えた。星の光が暗くなっても星の数が増えるので両者の効果が打ち消し合うことには考えが及ばなかった。

また、ケプラーもこの問題に気づき、星々が太陽と同じような星ならば、それらすべての星の光を合わせても夜空が暗く見えるのはなぜだろうか、と考察している。

ケプラーの場合は、星々が無限の彼方まで続いているとは考えていなかったため、単に星の数が全天を覆うほどには存在していないのだと考えた。

さらに、ハレー彗星の軌道計算をしてこの彗星の名前の由来ともなったことで有名なエドモンド・ハレーは、ニュートンの考えた無限に続く宇宙を支持して、この問題について考えている。

ただし、彼の場合は遠方にある星の数の見積もりをするところで誤りを犯し、間違って遠方の星は十分に増えないので夜空が暗いのだという結論を出してしまった。

オルバースのパラドックスをはっきりとした形で示したのは、スイスの天文学者、ジャン＝フィリップ・ロワ・ド・シェゾーである。1744年に出版した著作の中で、彼はオルバースのパラドックスの内容をはっきりと示している。

オルバースがパラドックスの内容を論じたのは、シェゾーより約80年も後、1823年のことである。オルバースはハレーの議論について述べているが、シェゾーの著作については触れていない。

オルバースはシェゾーの著作を蔵書として持っていたため、シェゾーの議論を知っていたと考えられるのだが、なぜシェゾーに触れなかったのかはよくわかっていない。