デイヴィッド・サンプター（数学者）

 

成功、人気、富、自信を与えてくれる10の数式。その秘密を隠し持つ人々の集団こそが「秘密結社TEN」だ。彼らは何世紀も前から行政、金融、学界、最近ではテクノロジーの世界で実権を握り、私たちを意のままに操ったり助言したりしながら、裕福で自信満々な日々を送っているのだ！
人気数学者が、現代社会を動かす数式とその利用法についてユーモラスな切り口で語る『世界を支配する人々だけが知っている10の方程式――成功と権力を手にするための数学講座』から、読みどころをピックアップ！

 

冷静に判断を下す　――ベイズの定理

 

全員が数学や統計学のバックグラウンドを持つ金融トレーダーのチームを率いている私の友人マークは、最高のトレーダーが持つひとつの共通点に気づいた。新しい情報を処理し、それに対応する能力だ。何か出来事が起きたとき、新たな現実に合わせてすぐさま自分の理解を見直すことができるのだ。

 

トレーダーは、「この会社は翌四半期に必ず利益を上げる」とか、「あの新興企業はまちがいなく失敗する」とかいうように、物事を白黒で考えたりはしない。むしろ、「この会社が利益を上げる確率は34％」とか、「あの新興企業が失敗するリスクは90％」とかいうように、物事を確率で考える。そして、CEOがやめさせられたとか、その新興企業のベータ版がなかなか好評である、といった新たな情報が入るにつれて、34％から21％、90％から80％というように確率を絶えず見直していくのだ。

 

ギャンブル業界の知人のジェームズからも、似たような話を聞いたことがある。彼らは前章で紹介した賭けの数式の一種を用いているのだが、大金がかかっている関係上、最新のモデルが次のサッカーの試合に対して有効なのかどうかを、すばやく見直していく必要がある。たとえば、試合開始の1時間前に先発メンバーが変更になり、モデルの根底にある仮定が成り立たなくなったら？

 

「本物のトレーダーかどうかがわかるのはそういう時なんだ」とジェームズは言う。「本物のトレーダーは過剰反応しない。先発メンバーがひとり変わったくらいなら、賭けはまだ有効だ。2〜4人変われば、そこで初めて別の可能性を加味しはじめる。5人以上が変われば、賭けはお流れだ」

 

飛行機の揺れはなぜ恐れるに足りないか

 

こうした分析家の思考を学ぶには、まず感情的にストレスのかかる状況に身を置くことだ。安全な地上にいるときは、ほとんどの人が飛行機に乗るのはそう危険でないと理解している。旅客機が墜落して死亡する確率なんて、1000万にひとつもない。でも、空の上にいると、印象はだいぶ変わってくることがある。

 

あなたが経験豊富な旅行客で、100回は飛行機に乗ったことがあるとしよう。でも、今回のフライトは今までと違う。飛行機が降下しながら、今まで体験したことのないような音を立てて揺れている。隣の女性は息をのみ、通路の反対側の男性は膝をぎゅっと握り締めている。周囲の全員が明らかに怯えている。これが1000万にひとつの事故ってやつ？　最悪のシナリオがこれから待っているのだろうか？

 

数学者なら、このような状況で深呼吸をし、あらんかぎりの情報を集める。数学的表記で、飛行機が墜落する基本的な確率をP（墜落）と書く。Pは確率（probability）の頭文字で、「墜落」は（あなたが）墜落死するという最悪のシナリオを示す。統計的記録から、P（墜落）＝1/10,000,000、つまり1000万分の1であることがわかっている。

 

出来事どうしの依存関係を理解するため、P（揺れ|墜落）という表記を導入しよう。これは、飛行機がこれから墜落すると仮定した場合に、このような揺れを起こす確率を示す（「揺れ」は「飛行機の揺れ」、棒線は「以下を仮定した場合の」という意味）。なので、P（揺れ|墜落）＝1、つまり墜落の前には必ずひどい揺れがあると仮定するのは合理的だ。

 

また、P（揺れ|墜落しない）、つまり無事に着陸できるのにひどく揺れる確率も知っておく必要がある。ここでは、あなた自身の直感が必要になってくる。今回は今までの100回の同様のフライトのなかで、いちばん恐ろしいフライトだから、P（揺れ|墜落しない）＝1/100というのがあなたの最善の推定といえる。

 

これらの確率は役立つけれど、あなたが知りたがっている情報とは違う。あなたが知りたいのは、P（揺れ|墜落）、つまり飛行機がひどく揺れていると仮定した場合の墜落の確率だ。ベイズの定理を使うとその値が求められる。

 

 

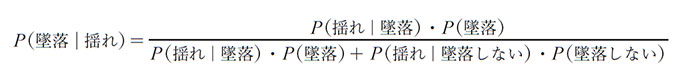
ここで、数式内の「・」記号は掛け算を表わす。現時点ではこの数式が正しいものとして受け入れよう。ベイズの定理は、18世紀中盤にトーマス・ベイズ牧師によって証明されて以来、幾多の数学者によって使われてきた。
この数式に数値を代入するとこうなる。

 

〔≈は「ほぼ等しい」の意〕

 

今まで経験したなかで最悪の乱気流だとはいえ、死ぬ確率は0.00001しかない。そう、無事に着陸できる確率は99.999％もあるのだ。

 

同じ推論は、一見すると危険に思えるさまざまな状況にも応用できる。オーストラリアの海辺で泳いでいるとき、水中に恐ろしい生き物が見えたと思っても、それがサメである確率は微小だ。愛する人の帰宅が遅れていて、連絡が取れないと、つい心配になってしまうけれど、ほとんどの場合は単なる携帯電話の充電のし忘れだろう。飛行機の揺れ、水中の怪しい影、つながらない電話など、私たちが新しい情報だと思っている物事の多くは、問題と正しく向き合えば、そこまで恐れるに足りない。

 

ベイズの定理を知っていれば、情報の重要性を正しく評価し、まわりのみんながパニックを起こしているときでも冷静さを保つことができるのだ。

 

社会科学を変えたベイズの推論――スマホは子どもの鬱の原因か

 

この数十年間で科学や社会科学のアプローチを一変させたベイズの推論は、世界をとらえる科学的手法と完璧に符合する。ベイズの法則は、実験家が収集したデータ（D）と、理論家が立てたそのデータに関する仮説やモデル（M）、そのふたつの要素を結びつけるのだ。

 

たとえば、こんな科学的仮説について考えてみよう―携帯電話の使用は、10代の子どもの精神衛生に悪い影響を及ぼす。これは私の家庭で盛んに議論されている問題だ。実際、私の家庭のふたりの子ども（と、公正を期すために言っておくと、ふたりの大人）は、一日じゅう携帯電話の画面とにらめっこしている。私が子どものころ、両親は私が今どこにいるのか、何をしているのかと四六時中心配していたけれど、今の妻と私の心配の種はそこじゃない。むしろ、子どもたちがずっと座り込んで、携帯電話の仄青い光を見つめてばかりいることのほうだ。「どうして門限までに帰ってこない？　今まで誰と一緒にいた？」という古きよきお小言は、私の家ではまず聞く機会がない。

 

社会学者で、子育てや生産性に関する自己啓発本を何冊か著わしているクリスティン・カーター博士は、携帯電話の使いすぎに断固反対し、「画面を見つめる時間こそが、おそらく10代の若者のあいだで急増している鬱、不安、自殺の元凶である」と記している。彼女はカリフォルニア大学バークレー校の『グレーター・グッド』誌内の論文で、その主張を2段階に分けて繰り広げている。第1段階で、彼女は親たちのアンケート結果を引用している。親の半数近くは子どもがモバイル機器に「依存」していると考えており、親の半数はそのことが子どもの精神衛生に悪影響を及ぼしていると心配していた。続く第2段階では、幸福感、人生への満足度、社会生活に関する14の疑問に答えたイギリスの12万115人の若者の調査データを引用した。調査の結果、たったの1時間を境に、スマホの使用時間が長い子どもほど、そのアンケートで測定された精神衛生の度合いが低かった。つまり、携帯電話を使えば使うほど不幸になるという言い方ができる。

 

説得力がありそうでしょう？　正直な話、初めてこの論文を読んだとき、私自身もすっかり納得してしまった。著者は博士号を持つ研究者。論文が発表されたのは世界最高峰の大学の雑誌。論文の主張を裏づける科学的な査読と厳密な調査データ……。ところが、そこにはひとつだけ問題、それも大きな問題が潜んでいる。

 

クリスティン・カーターは、判断の数式の上側の部分しか考慮していないのだ。第1段階は、親たちの不安について記述した部分で、ある親が、画面を見つめる時間が精神衛生に悪影響を及ぼすと考える確率P（M）に相当する。第2段階では、最新のデータが心配する親の仮説、つまりP（D|M）と一致していて、しかもこの値がかなり大きいことを示している。しかし、彼女が怠っていることがひとつある。現代の若者の精神衛生について説明しうるほかのモデルを、いっさい考慮していないのだ。彼女は数式（2）の分子（上側の部分）こそ計算しているのだが、分母（下側の部分）については言い忘れている。別の仮説に対するP（D|M^c）については何も言っていない。そのため、私たちが本当に知りたいP（M|D）の値、つまり携帯電話の使用が若者の鬱の原因である確率について、理解を深めてくれるわけではないのだ。

 

「判断の数式」が教えてくれること

 

カーターの放置した穴を埋めたのは、カリフォルニア大学アーバイン校の心理科学教授、キャンディス・オジャーズだった。彼女は学術誌『ネイチャー』に発表された解説で、まったく別の結論に達した。彼女は冒頭で、まず携帯電話の問題について認めた。アメリカでは、抑鬱を報告する12〜17歳の少女の割合が、2005年の13.3％から2014年には17.3％まで増加しており、同じ年齢の少年についてもそれより小さな数字ではあるが増加が見られる。一方、同期間で携帯電話の使用が増加したことは、ほぼ疑いようのない事実だ。統計を引っ張り出してくるまでもない。オジャーズはまた、クリスティン・カーターが引用したイギリスの若者の調査データに異論はなかった。携帯電話のヘビーユーザーのあいだで鬱の症例が増加することは確かだった。

 

オジャーズが指摘したのは、ほかの仮説によっても若者の鬱の増加は説明できるという点だった。毎朝朝食をとらない、睡眠時間が日によって違う、といった要因は、携帯電話の使用時間と比べて、精神衛生の悪化を予測するうえで3倍も重要だった。ベイズの定理の用語を使うなら、朝食と睡眠は鬱を説明しうる代替モデルであり、しかもこれらの確率P（D|M^c）は高い。これらのモデルをベイズの法則の分母に代入すると、分子を大きく上回り、携帯電話の使用が鬱と関係している確率P（M|D）は小さくなる。完全に無視できるわけではないが、若者の精神衛生の問題の重要な説明を提供するには足りない程度の小ささにはなる。

 

それだけではない。なんと、若者には携帯電話を使用するメリットがあることも実証されている。数々の調査で、子どもは携帯電話を使って互いに支え合い、長期的な社会的ネットワークを築くことが証明されている。携帯電話の使用時間について注意を受けることが多い中流階級の子どものほとんどにとって、携帯電話はオンラインだけでなく実生活においても、長く続く真の友情を築く能力を向上させるのだ。問題があるのは、キャンディス・オジャーズが論文内で示したとおり、恵まれない境遇の子どもたちだ。あまり裕福でない若者たちは、ソーシャルメディア上の揉め事に巻き込まれてしまう可能性が高い。また、実生活でいじめを受けたことがある子どもたちは、その後、オンラインで被害者になりやすいこともわかっている。

 

よくよく考えると、私の子どもたちは世界じゅうの人々とつながっているし、オンラインで新しい考えについて学ぶ機会も多い。あるときなんて、エリスとヘンリーがボンゴや文化の盗用について議論しているのを耳にしたこともある。

 

「誰かの文化の音楽を演奏していて、ムカつくと言われたら、やめるのが基本的な礼儀でしょ」とエリスは言った。
「じゃあ、エミネムも文化を盗用してるってこと？」とヘンリーは反論した。

 

私と姉が13歳と15歳のとき、果たしてこんな議論ができただろうか？　そうとは思えない。今だって自信がないくらいだ。2000年代生まれの子どもたちは、1970年代、1980年代、そして1990年代生まれの人々には理解できないような重要な考えや情報を理解できるのだ。