自分の悪口を偶然聞いてしまった！そんなとき咄嗟にとるべき行動とは？

ryomiyagi

2022/10/26

デイヴィッド・サンプター（数学者）

成功、人気、富、自信を与えてくれる10の数式。その秘密を隠し持つ人々の集団こそが「秘密結社TEN」だ。彼らは何世紀も前から行政、金融、学界、最近ではテクノロジーの世界で実権を握り、私たちを意のままに操ったり助言したりしながら、裕福で自信満々な日々を送っているのだ！
人気数学者が、現代社会を動かす数式とその利用法についてユーモラスな切り口で語る『世界を支配する人々だけが知っている10の方程式――成功と権力を手にするための数学講座』から、読みどころをピックアップ！

自分の悪口を言った女性が「性悪」である確率

大学で新しい授業が始まった。学生のエイミーは、ある悩みを抱えている。誰と仲良くすればいいの？　誰とは距離を置いたほうがいいかしら？　彼女は人を信じやすい性格で、彼女の頭のなかでは、ほかの人々が自分を受け入れて優しくしてくれる映画が流れている。でも、彼女は完璧なお人好しではない。今までの経験から、みんながみんないい人ばかりでないことも知っていて、彼女の頭のなかでは「性悪女」の映画も流れている。おっと、この言葉遣いで彼女の性格を判断しないであげてほしい。口に出しているわけではないから。さて、たまたま隣に座ったレイチェルという女の子と知り合ったとき、エイミーはレイチェルが「性悪女」である確率をかなり低く、たとえば20分の1くらいに見積もった。

エイミーが誰かと会うたびに「性悪女」の確率を厳密に設定しているとは思わない。私がここで数値を定めたのは、この問題をとらえやすくするためだ。あなた自身も少し立ち止まって、あなたの知り合いの何割くらいが性悪女かを考えてみてほしい。たぶん20人にひとりもいないと思うけれど、あなた自身で好きな値を選んでかまわない。

初日の朝、レイチェルとエイミーは、ふたりでその講座の学習課題を見直していた。エイミーはそれまでの学校で、その講師が使っている概念を習っていなかったので、細かい点を飲み込めずにいる。レイチェルはエイミーのペースに合わせてくれているけれど、ちょっとだけイライラしている様子が伝わってくる。どうしてエイミーはこんなに飲み込みが悪いの？　すると昼食後、恐ろしい出来事が起こる。エイミーがトイレの個室で座り、黙々と携帯電話を観ていると、レイチェルと別の女の子が入ってくるのが聞こえる。
「あの子、本当にバカなの」とレイチェルは言う。「私が“文化の盗用”〔ほかの文化の要素を流用する行為。特に多数派民族の人々が少数派民族の文化を、背景を無視したまま勝手に私物化してしまう行為〕について説明しようとしたんだけど、ポカンとしているのよ。ボンゴの演奏方法を学ぼうとしている白人のことを言っていると思ったみたい！」

エイミーは黙ってじっと座り、ふたりが帰るのを待っている。さて、この出来事についてどう考えるべきだろう？

ほとんどの人は、エイミーの立場だったら、悲しくなったり、腹が立ったりするだろう（その両方かも）。でも、その反応は正しいのだろうか？　確かに、レイチェルのしたことはよくない。エイミーにとっては初日だし、あんなふうに人の悪口を言うのはよくない。ただ、問題は、レイチェルの罪を許し、もういちどチャンスを与えるべきかどうかだ。

答えはイエス、絶対にイエス、何がなんでもイエスだ。許したほうがいい。いや、許すべきだ！　それも今回かぎりではなく、何度かは。ひどい発言をした人、本人がいると気づかずに陰口を叩いた人を、ぜひ許してあげたほうがいい。

なぜか？　お人好しになるべきだから？　心を踏みにじられても我慢するべきだから？　人間は自分を守るために声を上げられない弱い生き物だから？

いやいや、そうじゃない。まったく違う。そのほうが合理的だからだ。論理や理屈に適っているからだ。公平だからだ。ベイズ牧師がそう言っているからだ。第2の数式によれば、それが唯一の正しい道なのだ。

その理由はこうだ。ベイズの定理は、モデルとデータの橋渡しをしてくれる存在であり、私たちの思い描く映画が現実とどれくらい一致するのかを判定するのに役立つ。本章の冒頭の例で、飛行機が激しく揺れている場合の墜落の確率P（墜落|揺れ）を求めた。エイミーが知りたがっているのはP（性悪女|悪口）だが、理屈はまったく同じだ。
「墜落」と「性悪女」は、私たちの頭のなかにあるモデルだ。いわば世界に対する私たちの信念であり、思考（私の場合は映画）という形を取る。一方、「揺れ」と「悪口」は、私たちの眼前に存在するデータだ。データは、実際に触り、体験し、感じることのできる具体的な出来事だ。応用数学の大部分は、モデルとデータ、私たちの夢と厳しい現実、それをすり合わせることで成り立っている。

モデルをM、データをDと表記しよう。今、私たちが知りたいのは、手元のデータ（トイレ内での失礼な発言）を仮定した場合に、私たちのモデルが正しい（レイチェルが性悪女である）確率だ。

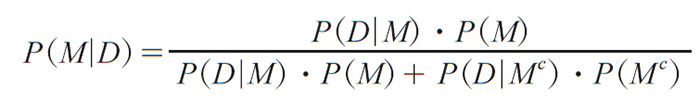
この数式―ベイズの定理―を理解するには、右辺を分解してみるのがいちばんだろう。

分子（右辺の分数の上側の部分）は、P（M）とP（D|M）のふたつの確率を掛けたものだ。ひとつ目のP（M）は、何も起きていない段階で、あるモデルが正しい確率を示す。つまり、飛行機が墜落する統計的確率や、出会った人が性悪女であるエイミーの推定確率のことだ。後者はエイミーがトイレに行く前の段階で推定していた確率であり、具体的には20分の1だ。ふたつ目のP（D|M）は、トイレ内での出来事に関する確率であり、レイチェルが本当に性悪女であった場合に、トイレ内でエイミーの悪口を言う確率を表わす。もう少し一般的にいうと、モデルが正しい場合にそのデータが観測される確率を指している。数値を割り当てるのは難しいけれど、半々と考え、P（D|M）＝0.5としておこう。レイチェルが性悪女だとしても、トイレに行くたびにクラスメートの悪口を言うわけがない。性悪女でも、最低50％は別の話をするはずだ。

分子でふたつの確率の積P（D|M）・P（M）を取る理由は、ふたつの事象が両方とも成り立つ確率を求めるためだ。たとえば、2個のサイコロを振って、両方とも6が出る確率を知りたければ、1個目のサイコロが6である確率1/6と、2個目のサイコロが6である確率1/6を掛ければよい。その結果、ふたつとも6である確率は1/6・1/6＝1/36となる。同じ掛け算の原則がここでも成り立つ。分子は、レイチェルが性悪女であり、かつトイレで意地悪な発言をする確率だ。

数式（2）の右辺の分子は、レイチェルが性悪女であるケースについて考えるものだが、レイチェルがいい人であるという別のモデルについても考えておかなければならない。それが分母（分数の下側の部分）の役割だ。レイチェルは意地悪な発言をする性悪女（M）か、うっかり意地悪な発言をしてしまったいい人（M^c）か、そのふたつにひとつだ。Mの右上についている小さなcは、補集合（complement）を指す。この場合の補集合とは、彼女が「いい人」であるケースだ。お気づきのように、分母の第1項のP（D|M）・P（M）は分子とまったく同じだ。そして、第2項のP（D|M^c）・P（M^c）は、レイチェルが性悪女ではないのに意地悪な発言をする確率と、人々が一般的にいい人である確率を掛けたものだ。すべてのケースの和で割ることによって、エイミーがトイレの個室で観測したデータについて考えうる説明をすべて網羅し、特定のデータが与えられた場合にモデルが正しい確率P（M|D）を求められる。

レイチェルが性悪女でなければ、いい人ということになるので、P（M^c）＝1−P（M ）＝0.95となる。ここで、いい人がうっかり意地悪な発言をしてしまう確率について考える必要がある。レイチェルは実際にはいい人なのに、たまたま機嫌が悪かっただけかもしれない。誰だってそんな日はあるだろう。そこで、P（D|M^c）＝0.1としよう。これは、機嫌が悪いせいで、いい人があとで後悔するような発言をしてしまう日が、10日に1日あることを示している。

一つひとつの出来事に落胆するな

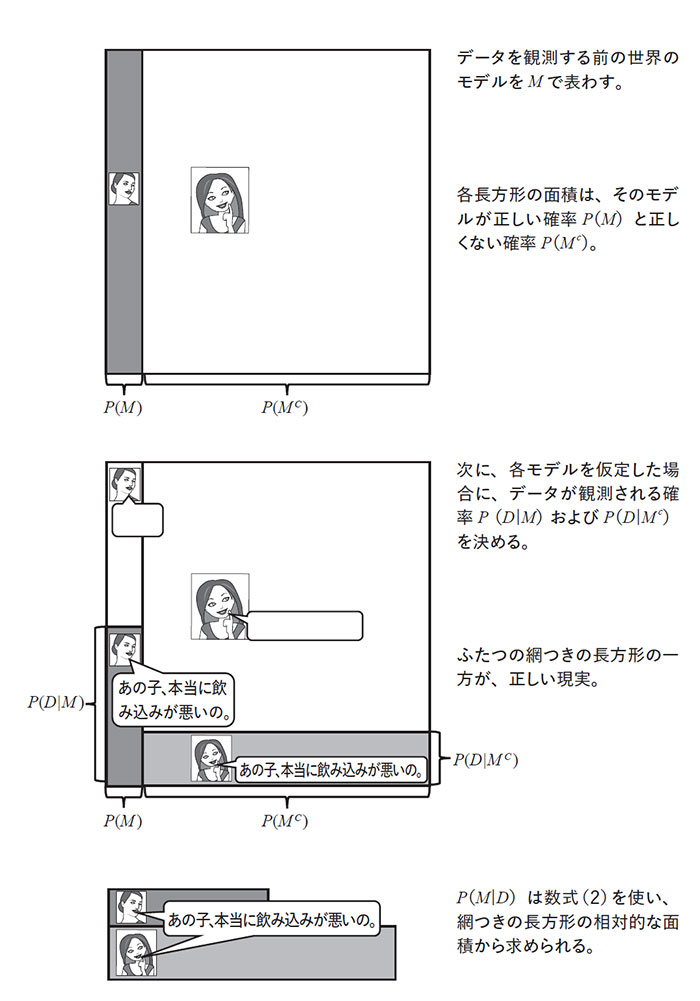
さあ、あとは計算だ。その計算を図示したものが次頁の図2だ。計算方法は飛行機の墜落の例とまったく同じだが、数値が違っている。

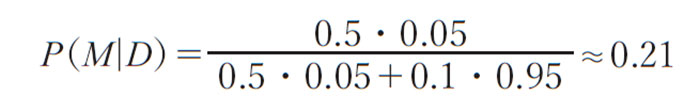
つまり、レイチェルが性悪女である確率は5分の1くらいしかない。彼女を許すべきだと言ったのは、そういうわけなのだ。彼女がいい人である確率は5分の4もある。今回のたった1回の行為で彼女の人間性を判断するのは完全に不公平だというのがわかる。トイレのなかで聞いたレイチェルの発言を蒸し返すべきではないし、その発言によってレイチェルへの接し方を変えるべきでもない。明日、また様子を見るべきなのだ。年度末を迎えるころには、トイレの個室での事件について、ふたりで大笑いしている可能性は80％もあるのだから。

もうひとつ、トイレの扉の後ろで息を殺していたエイミーに対して、アドバイスがある。確かに、トイレで自分の悪口を聞いた日の朝、彼女にも抜かりがあったのかもしれない。ふたりで勉強しているとき、もう少しきちんと集中したほうがよかったかもしれないし、正直な話、昼食後に長々とトイレに座って携帯電話をいじっていたのがいけなかったのかもしれない。でも、ベイズは罪を許すということを忘れないでほしい。レイチェルだけでなくエイミー自身に対しても、同じ原則が成り立つのだ。ベイズの定理はこう教えてくれる。自己評価は少しずつ見直していけばいい。一つひとつの出来事にそう落胆する必要なんてない、と。

あなたという人間は、ひとつやふたつの失敗ではなく、あなたのすべての行動でできている。ベイズはほかの人々を許しなさいと言っている。その合理的な許しを、あなた自身にも与えてみてはどうだろう。